摘要 摘要:采用有限元方法分析出涡轮风扇支板个数为10时发生断裂的原因是高周疲劳破坏,并且叶片发生疲劳的主要原因是支板个数设置不合理.通过Campbell图分析出了两种优化方案,即支
摘要:采用有限元方法分析出涡轮风扇支板个数为10时发生断裂的原因是高周疲劳破坏,并且叶片发生疲劳的主要原因是支板个数设置不合理.通过Campbell图分析出了两种优化方案,即支板个数为3和19.从共振点个数、应力水平及理论寿命来看,支板个数为19均优于3.分别对支板个数为10和3的叶片进行疲劳寿命模拟计算,结果表明,两者的疲劳寿命均较短,不符合工程实际要求,最终确定支板个数19为优化方案.
关键词:涡轮风扇叶片;支板;振动;疲劳;优化设计
0引言风扇在航空涡轮增压器[1]中的主要作用是为压气机散热,其包括风扇导流环、支板、风扇叶轮、风扇罩等.在工作过程中,风扇与涡轮同轴连接,随着涡轮轴的转动而转动,涡轮风扇工作时具有转速高、转速变化范围较宽、形体单薄、气动载荷较大及热载荷大等特点[2],因此涡轮风扇叶片出现故障的次数较多,其工作状态和使用年限直接影响涡轮增压器的故障发生.目前,对于叶片与轮盘振动破坏及疲劳分析时,徐可宁等[3]利用三维叶轮机械气动弹性分析软件AEAS,对某压气机转子错频叶盘结构进行了振动响应分析,吴承伟等[4]采用疲劳分析方法对离心式叶轮叶片进行了寿命计算并提供了一种计算方式,得出影响离心压缩机叶片寿命的因素包括稳态平均应力及交变应力.
金鑫[5]等采用通用动态尾流理论进行风力机气动力学计算,对叶片进行加载分析,得出风力机系统振动耦合分析.关振群等[6]对闭式叶轮的振动特性及叶轮的疲劳寿命提出了运用有限元的方法对其进行计算.总之,国内大多数研究人员对叶片进行振动破坏及疲劳寿命分析时,主要是利用单一的求解方法,很少能够全部采用有限元数值方法对叶片进行振动特性分析及疲劳寿命计算,进而优化结构.
基于上述原因,本文在动强度及疲劳分析理论基础上,运用ABAQUS对涡轮风扇叶片进行分析,并采用Campbell图得出了两种优化方案,通过进行激振力模态分析及疲劳寿命计算,最终确定出较合理的优化方案.
1涡轮风扇动强度分析
1.1风扇有限元模型建立
涡轮风扇由叶轮和导流罩两部分组成,导流罩外壁与内壁之间通过10个支板连接.其中叶轮由17个叶片组成,考虑到整体模型划分网格时工作量大的问题,依据整体模型具有循环对称性的优势,取整体模型沿着周向的1/17扇形(单只叶片)作为基本模型,这样能有效降低计算时间,提高分析效率.模型建立过程中,由于所提供的IGS格式几何文件中的模型为壳体,需将几何模型导入UG中,选择合适的公差将涡轮风扇缝合为实体,建立成单只叶片的模型.之后采用通用CAE前处理软件Hypermesh建立风扇的有限元模型,即将取出的单只叶片导入Hypermesh中进行单只叶片有限元网格划分,共计14162个单元,17880个节点.具体模型见图1.
1.2材料属性和边界条件
(1)材料属性风扇选用材料为钛合金,由于计算过程中不考虑热应力的作用,忽略材料随温度的变化,取钛合金(TC4)在常温下的材料属性,钛合金参数见表1.

(2)边界条件
涡轮作为动力,通过轴的传动带动风扇转动,在施加边界条件时需要将轴孔处的所有节点x、y和z方向位移固定,即:U1、U2和U3同时为0,同时选定转轴Z轴,沿着Z轴方向创建2个基准点,作为旋转方位,施加周期性边界条件,叶片数为17,并且施加循环对称约束边界条件,如图2所示.

1.3载荷与动强度分析
1.3.1载荷
计算动强度时需要在ABAQUS中给定转速10、25000、45000、50000、52000、60000rpm;叶片设置了10个支板,空气经过导流罩入口,经过支板流向风扇叶轮,由于支板的存在导致流过叶片的空气不均匀,风扇叶片每旋转一周,这种不均匀性的气体作用一次,从而产生了周期性的气流激振力,设气流激振力的频率[7]为
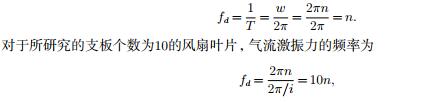
式中n为风扇叶片的转速,单位r/s;i为支板个数,取10;T为气流激振力的周期,单位s;w为激振力的圆频率,单位rad/s.气流激振力的计算结果,通过NUMECA可以得出,取为800Pa.
1.3.2动强度分析将给定转速与气流激振力加载到叶片模型上之后进行模态分析,具体结果见表2.

为了进一步研究叶片的共振特性,得出共振点转速与共振频率,确定低阶次频率之后,还要考虑与支板个数相等的动频、与风扇叶片数相等的动频阶次以及风扇叶片个数与支板个数之差相等的动频阶次.根据表2绘制了Campbell图,见图3.
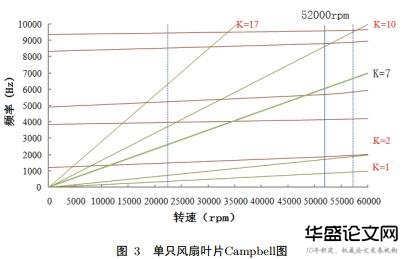
图3中主要关注17倍频(K=17,17为风扇叶片个数),10倍频(K=10,10为支板个数),7倍频(K=7,7为风扇叶片个数与支板个数之差),1倍频和2倍频.同时垂直横轴设有一条实线和两条虚线,实线代表涡轮风扇叶片的工作转速范围内的最大值52000rpm.两条虚线表示安全裕度,左侧虚线代表工作转速范围内最小值25000rpm的85%,即21250rpm,右侧虚线代表超过工作转速范围内的最大值52000rpm的10%,即5200rpm.
判断单只风扇叶片共振分析时,只要倍频线与基频线的交点出现在转速波动范围内,即产生共振,该交点就是共振点,通过共振点可确定发生共振时的频率与转速.表3就是通过图3确定的共振转速.
从图3的Campbell图和表3可以看出,在工作转速范围内,共有六个共振转速.由支板个数(10)带来的激励源,使叶轮存在三个共振转速:与二阶模态对应的转速为24006rpm,与三阶模态对应的转速为32706rpm,与四阶模态对应的转数为53234rpm;由风扇叶片数(17)与支板(10)的差数7带来的激励源,其共振转数有两个:二阶模态时相应转速34850rpm,三阶模态时相应转速48975rpm;而由风扇叶片数(17)带来的激励源,其共振转数有一个:与四阶模态对应的转数为30489rpm.六个共振转速中,模态为弯曲振型最危险,即转速32706rpm和转速48975rpm是最危险的共振转速.

在最危险共振转速工况下对叶片进行静强度分析,结果见图4.
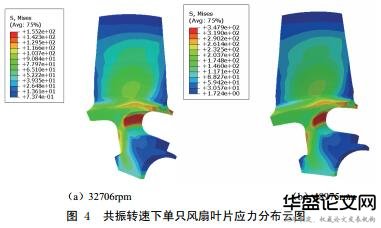
在共振转速48975rpm下的应力大于共振转速32706rpm产生的应力值,对照S-N曲线可知,应力S越大,疲劳寿命N越短,高周疲劳(应力疲劳)破坏产生,因此共振转速48975rpm是更加危险的工况.
从上述分析过程中不难看出,风扇叶片个数、支板个数及两者差别均会带来激振源,其所产生的共振更会造成风扇叶片累计损伤.所以在调整风扇叶片个数较困难的情况下,由支板个数不合理导致风扇叶片在其工作转速范围内存在共振点的个数过多,即使当风扇工作在共振转速附近时可以通过人为控制,但由于共振点个数过多,也很难实现,由此证明支板个数为10是不合理的.
2风扇结构优化设计
2.1确定优化方案
针对支板个数为10的风扇叶片分析中出现的问题,确定支板个数为奇数时更能满足17只叶片的工作要求,同时从图3中可以看出,考虑避开风扇共振区域,只能在共振区域两端进行选择,所以最终将支板个数调整为3个和19个,并分别对其进行对比分析,确定最优方案.
2.2优化模型动强度分析
在计算优化模型过程中,分析步的设置与原模型只需将加载气流激振力调整为18000Pa和25000Pa即可.
2.2.1支板个数分别为3和19时,涡轮风扇动强度分析
由于只考虑单只风扇叶片是否会发生共振,所以根据计算结果直接绘制Campbell图.
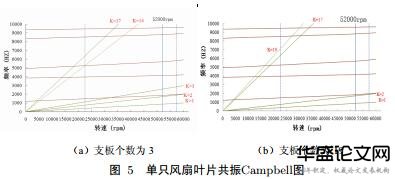
图5中,支板个数为3的存在5个共振点,而支板个数为19的存在4个共振点,每个共振点下计算出的共振转速与共振频率见表4、5.
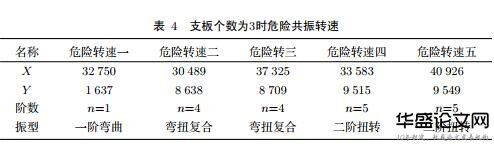
利用表4得出支板个数为3时,存在五个共振点:危险转速一(32750rpm)是由支板个数3导致的;危险转速二与危险转速五则是由叶片个数17与支板个数3导致的,即与14倍频线有两个交点;危险转速三(37325rpm)与危险转速四(33583rpm)是由叶片个数17导致的.其中,一阶弯曲在五个共振点中是最危险的,最终确定了最危险共振转速37250rpm.
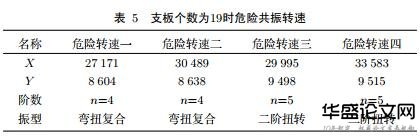
通过表5分析可得,虽然支板个数为19时,仍然会出现4个共振点,但是在这4个共振点发生的振型中并没有出现弯曲振型,因此相比其他支板个数有明显优势,但仍需要进行强度分析.弯扭复合与二阶扭转相比,对风扇叶片产生的疲劳损伤更为严重,因此在以上4个共振点中我们确定危险转速二是最危险的情况,此时共振转速为30489rpm.
在最危险共振转速工况下对叶片进行静强度分析,结果见图6.
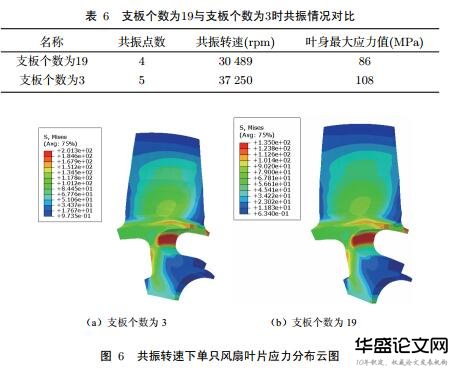
从图6和表6中可以看出,支板个数为19与支板个数为3时均存在共振的情况,但支板个数为19的共振转速和共振时产生应力值均小于支板个数为3的情况,同时对照S-N曲线可知,应力S越大,疲劳寿命N越短,支板个数为19的寿命均高于支板个数为3的寿命.
3疲劳寿命计算
3.1疲劳寿命计算模型
选择的计算模型与前面动强度计算相同,而且由于整个运算过程相同,通过共振分析确定支板个数为19的寿命均高于支板个数为3的寿命.为了避免重复,只对支板个数为10和3的叶片进行疲劳寿命分析,运用fe-safe与ABAQUS联合计算,选出合理的优化结构.
3.2高周疲劳载荷谱确定
涡轮风扇叶片高周疲劳载荷谱由应力均值σL和高周应力幅值σa两部分组成,其中应力均值σL是由涡轮风扇叶片在离心力载荷与稳态气流力载荷作用确定的应力值,而高周应力幅值σa是气流激振力产生的扰动应力.但同一个风扇叶片上,应力均值σL和高周应力幅值σa并不是出现在同一位置,为了安全考虑,以最危险工况为准,将其视为发生于同一点,于是确定风扇叶片的高周疲劳载荷谱.图7是一个循环周次下高周疲劳载荷谱.
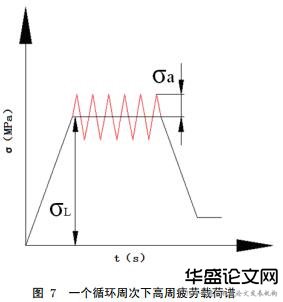
3.3疲劳计算结果分析
(1)支板个数为10时疲劳寿命
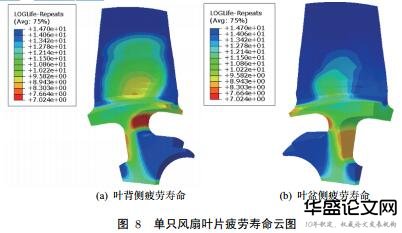
图8显示,风扇运转过程中疲劳寿命最短处发生在叶身处,通过线性化得出支板个数为10的涡轮风扇叶片在经过1.47×109周次的循环后,风扇叶片的根部即发生了疲劳断裂,最先发生断裂的位置是在第7419单元1号节点位置,该位置也是叶片叶身最大应力处,发生断裂时共振的频率是1487Hz,折算后约为85h,也就是支板个数为10时,在发生共振情况下,涡轮风扇叶片在运转85h后出现了疲劳断裂.
(2)支板个数为3时疲劳寿命
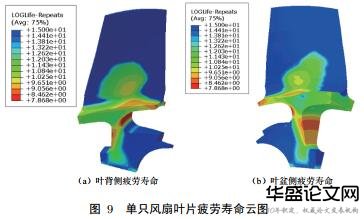
图9中,风扇叶片最短疲劳寿命发生的位置与支板个数为10时相同,疲劳寿命分布状况基本一致,而支板个数为3时疲劳寿命有了较大提高,经测得风扇叶片叶身处的最短寿命为2.73×109周次,转化后约为153h.
从以上数据中可以看出,支板个数为3时疲劳寿命虽有高于支板个数为10的情况,但两者均较短.因而对于涡轮风扇而言,风扇叶片是其核心部件,设计时采用的是无限寿命设计方法,要求其寿命较长,但是通过上述两种情况的对比分析,不难发现,支板个数为3的优化方案仍然不能满足要求,结合S-N曲线分析,最终确定采取支板个数为19的优化方案.
4结论
(1)对支板个数为10的风扇叶片进行动强度分析,结果表明,风扇叶片个数、支板个数及两者差别均会带来激振源,其所产生的共振更会造成风扇叶片累计损伤,进而使叶片产生高周疲劳破坏,且共振点个数较多,即支板个数为10是不合理的.
(2)分别对支板个数为3和支板个数为19的涡轮风扇进行动强度分析,结果显示,支板个数为19时,单只风扇叶片出现的共振点是4个,与支板个数为3时相比共振点的个数减少,应力水平较低,寿命较高,不会出现高周疲劳破坏,支板个数为19的方案较优.
(3)对支板个数为10和3的叶片进行疲劳寿命模拟计算,结果得出,支板个数为3时疲劳寿命虽高于支板个数为10的情况,但两者均较短,不符合实际工作要求,优化结构选择支板个数为19的方案.
参考文献:
[1]宋凯,刘堂先,李来平,等.航空发动机涡轮叶片裂纹的阵列涡流检测仿真[J].航空学报,2014,35(8):2355-2363.
[2]苏清友.航空涡喷、涡扇发动机主要零部件定寿指南[M].北京:航空工业出版社,2004:181-195.
[3]徐可宁,王延荣.压气机转子错频叶盘结构振动响应分析[J].燃气涡轮试验与研究,2013,26(3):6-11.
[4]吴承伟,关振群,郭杏林.大型离心压缩机叶轮叶片疲劳可靠性分析[J].装备制造技术,2008,8(1):1-3.
[5]金鑫,何玉林,杜静.风机结构耦合振动分析[J].中国机械工程,2008,19(1):9-13.
[6]关振群,王鄢,杨树华.大型离心压缩机闭式叶轮动力特性分析[J].大连理工大学学报,2012,52(3):320-326.
[7]曲震,柳恺骋.基于周期对称的大小叶片叶盘振动特性分析[J].滨州学院学报,2015,31(2):32-37.
转载请注明来自:http://www.lunwenhr.com/hrlwfw/hrgylw/9242.html