摘要 摘 要:Ⅱ型折线形实用堰广泛应用于中小型水利工程中,但不同水头和堰高比值下、不同堰体形式下的流量系数尚未有全面准确的解答方案。 针对工程中常用的上下游坡度(0.5~ 3.0)堰
摘 要:Ⅱ型折线形实用堰广泛应用于中小型水利工程中,但不同水头和堰高比值下、不同堰体形式下的流量系数尚未有全面准确的解答方案。 针对工程中常用的上下游坡度(0.5~ 3.0)堰体,通过室内水工模型试验,对相对堰高H/ P1值在 2~ 5、相对堰顶厚度 δ / H 值在 1~ 2.5 情况下的Ⅱ型折线形实用堰的流量系数进行了测定;并利用相关性分析、线性回归方法,整理推导出一套简单实用的Ⅱ型折线形实用堰流量系数计算方法,可为工程设计提供依据和参考。
关键词:折线形实用堰;流量系数;计算方法;线性回归;相关性分析
Ⅱ型折线形实用堰具有结构简单、造价低廉、就地取材的特点,在低水头闸坝引水枢纽工程和农田水利工程中得到广泛应用,其流量系数是工程设计的重要参数。 但在实际工程中,由于受到过流能力、填筑材料以及堰体自身稳定等因素的影响,从而形成了不同体型、不同水流条件的堰体,对于Ⅱ型折线形实用堰流量系数的选取,相关文献和设计手册还未能精准而全面的给出确定的方法,从而导致设计人员在取值时产生较大的偏差。 从众多的工程实例分析可以看出,现有的计算方法偏于保守,即实际的过流能力大于计算的过流能力,进而使得设计情况与工程实际过水能力大不相符,造成了实际工程规模偏大[1]。 基于此现状,以工程实践中常见的堰体形式为研究对象,通过室内水力学模型试验进行流量系数的测定,并利用数学工具进行数据分析,整理并推导出一套简单实用的Ⅱ型折线形实用堰流量系数计算方法,可为类似工程提供设计依据和参考。
1 试验概况
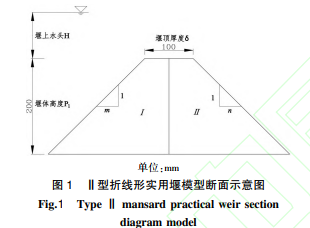
根据实际工程中常用折线形实用堰的水头、堰高、堰顶宽以及水力特征等因素,结合实验室供水能力、试验水槽尺寸、量测手段等现实条件,试验采用正态模型,按照重力相似准则进行设计。 确定几何比尺 λl= 15,共制作 11 组堰体模型,材料为聚氯乙烯板,堰体高度 P1均为 20 cm,堰体宽度 B(垂直水流方向)均为 40 cm,堰顶厚度 δ(顺水流方向)均为10 cm。 试验模型分别由上游Ⅰ和下游Ⅱ两部分堰体组成,每部分堰体由顶盖、底板、坡面、两侧立板等构件组成,上、下游坡比分别为: 1 ∶ 0.5、 1 ∶ 1.0、1 ∶ 1.5、1 ∶ 2.0、1 ∶ 3.0及其不同组合[2-3]。 堰体模型断面如图 1 所示。
试验在明渠水槽中进行,堰体流量系数 m由理论公式 Q = εσmB 2gH3/ 20 计算得到。 公式中堰体宽度 B = 40 cm,侧收缩系数 ε = 1.0,堰体下游保持自由出流状态 σ = 1.0,H0 计算公式为: H0= H + αv22g,H、Q 两个参数由试验测定,本次试验中堰上水头范围为 0 ~ 9.66 cm,堰上水头 H 在堰体上游距堰体 35 cm 处采用水位测针进行量测,过堰流量 Q 采用水槽末端矩形量水堰量测。 在量测堰体顶部水头H 时,每个堰型堰上水位进行 6 ~ 8 次调整,调整范围约为 1~2 cm,每个水位下重复量测 5 次,取平均值作为本次水位数值[4]。
2 试验结果
试验中, 堰体上游水槽 内 流 速 为 0.10 ~ 0.15m / s,其对应流速水头0.5 mm≤ αv22g ≤0.8 mm。 因此忽略了行近流速对堰体过流的影响,取 H0= H ,经计算得到不同形式堰体(上游边坡系数 m,下游边坡系数 n)的流量系数。 表 1 列出了 m = 0.5,n = 0.5、1.0、1.5、2.0、3.0不同堰体的计算结果。
从表 1 中可以得到:对于Ⅱ型折线形实用堰流量系数 M 值变化范围为0.384 ~ 0.465;且在一定水头范围内,流量系数随着堰顶水头的增大而增大,随相对堰高 H/ P1(堰顶水头/ 堰高)的增大而增大;并随着相对堰顶厚度 δ / H(堰顶厚度/ 堰顶水头)的增大而减小,此趋势与文献[7]所述一致。
3 流量系数计算方法
3.1 流量系数影响因素的讨论
文献表明[5]:梯形断面堰流量系数,一般介于宽顶堰与曲线型实用堰之间,其值约为0.33 ~ 0.46,并随相对堰顶厚度(δ / H)、相对堰高(P1/ H)和前后坡比的不同而异。相对堰顶厚度对堰流的分类具有决定意义,实用堰的应用范围为:0.67<δ / H<2.5;文献[6]提出了折线型实用堰的堰型判别界限为:0.67 <δ / H< 2.5,且0.5≤P1/ H。 本试验中相对堰顶厚度1.0≤δ / H<2.5,根据折线型实用堰自由泄流的流量系数计算的经验公式 M = m0+ C(δ / H) :H.H.巴甫洛夫斯基公式、别列津斯基公式、Govinda Rao 和 Muralidhar 公式,其公式适用范围:δ / H = 0.5 ~ 2.5(H.H.巴甫洛夫斯基公式为2.0),因此分析时相对堰顶( δ / H) 不再细化分段讨论。上游相对堰高(P1/ H)对堰流流态也有着不可忽略的影响。 试验中 P1/ H 的分布在 2 ~ 5 之间。对 P1/ H 在不同区间[2,3)、[3,4)、[4,5) 对流量系数的影响进行了假设检验,结果表明当区间划分为[2,3)、[3,5)时,规律具有较强的一致性。 沿用习惯表达,在分析中采用了 H/ P1作为控制指标[7]。对于梯形实用堰上游贴坡后流量系数将会增加,而堰体下游越缓,流量系数也随之变小。 工程设计中在保证堰体稳定情况下,从提高泄流能力和不致过大增加工程量的前提出发,根据上游堰体坡度较陡,下游坡度相对较缓的特点,参考工程实际,试验中堰体上下游坡度选择在0.5~3.0范围内。
3.2 流量系数的表达形式
文献[8]显示,实用堰流量系数的经验公式有M =m0+ C(H/ δ) 和 M = m0+ C H/ P1 ( ) 两类。 如上节对试验中相对堰顶厚度的讨论,确定 M = m0+C H/ P1 ( ) 为流量 系 数 的 表 达 形 式, 并 划 分 2.0 ≤ P1/ H<3.0,3.0≤P1/ H<5.0两个区间进行分析。
3.3 相关性分析
对试验结果进行相关性分析,结果显示上游坡比对流量系数有影响,但敏感性不强,因此对堰体下游坡比进行了两两的相关性分析。 结果见表 2。
从表 2 中结果可以看出:各组之间关系均为显著,即各组间的规律具有一致性;另外,从 Pearson相关系数可以看出它们之间存在显著的正相关性[9]。 因此,为使构造出的流量系数公式应用简单方便,采用 M = m0+ C H/ P1 ( ) 形式拟合,并引入参数 λ(调整系数)用于调整由于不同下游坡比所带来的差异,即初步构造流量系数公式为: M = λm0+C H/ P1 ( ) 。
3.4 流量系数计算方法
在基于流量系数与各因素关系的基础上,通过线性拟合方法,并考虑公式的应用方便,确定了 m0 、C、λ 参数值。 Ⅱ型折线形实用堰流量系数计算公式为:M = 0.324λ + 0.23 H/ P1 ( ) 。 (1)式中 λ 为调整系数,具体取值见表 3。
利用公式(1)和表 3 中的 λ 值计算得到流量系数 M 值与试验测量值最大误差为-3.7%,线性回归R2≥0.803。 说明利用此计算办法的精度可以满足应用要求。 另外,回归分析时调整误差(计算值-测量值)为负值,为工程设计应用预留一定的安全度。
4 结 论
(1)通过室内试验水工模型试验,测定Ⅱ型折线形实用堰流量系数范围在0.384 ~ 0.465之间,随相对堰顶厚度(δ / H)、相对堰高(P1/ H)和前后坡的不同而异。
(2)Ⅱ型折线形实用堰流量系数可利用公式M = 0.324λ + 0.23 H/ P1 ( ) 进行计算,公式适用范围: 1.0 ≤ δ / H ≤ 2.5 ; 2.0 ≤ H/ P1 ≤ 5.0 。参考文献:[1] 吴国君,刘晓平,方森松.低实用堰水力特性及其对工程的影响[ J]. 武汉:长江科学院院报,2011,28 ( 9):21-24.[2] SL155—95,水工(常规)模型试验规程[S].北京:中国水利水电出版社,1995.[3] 左东启.模型试验的理论和方法[M].北京:水利电力出版社,1988.
参考文献:
[1] 吴国君,刘晓平,方森松.低实用堰水力特性及其对工程的影响[ J]. 武汉:长江科学院院报,2011,28 ( 9):21-24.
[2] SL155—95,水工(常规)模型试验规程[S].北京:中国水利水电出版社,1995.
[3] 左东启.模型试验的理论和方法[M].北京:水利电力出版社,1988.
Ⅱ型折线形实用堰流量系数计算方法相关论文期刊你还可以参考:《非线性四阶差分方程的振动性》
转载请注明来自:http://www.lunwenhr.com/hrlwfw/hrsklw/11339.html